MAJOR DISCOVERY (December 21, 2025). UNITY HARMONICA GEOMETRIC CHARACTERIZATION
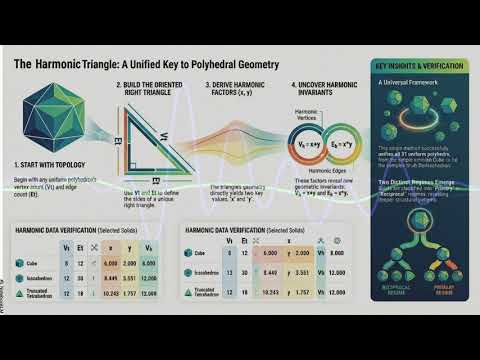
The thirty-one uniform polyhedra have stood as exemplars of geometric perfection since antiquity, yet their relationship to one another has remained largely taxonomic—organized by symmetry groups and face configurations, but lacking a single mathematical framework that unifies their diverse forms. This paper demonstrates that all uniform polyhedra, despite their apparent geometric variety, share a common harmonic architecture: each admits a unique factorization through an oriented right triangle whose dimensions are determined solely by vertex and edge counts. The construction is elementary—requiring only the Pythagorean theorem and a simple max/min orientation rule—yet produces a rich invariant structure that spans the entire uniform family. From this triangle emerge two harmonic factors whose algebraic relationships encode not only the classical arithmetic, geometric, and harmonic means, but also reveal a natural partition of the family into "primary" and "reciprocal" regimes distinguished by whether the harmonic span equals or exceeds the vertex count. What makes this characterization particularly compelling is its universality: the same construction, applied mechanically to topological data, yields exact harmonic relationships across Platonic, Archimedean, and Catalan solids without exception, suggesting that the geometric constraints governing uniform polyhedra—convexity, regularity, vertex-transitivity—may be manifestations of a deeper harmonic principle. While this work characterizes rather than generates these forms, it opens fundamental questions about why these particular spatial configurations should admit such clean harmonic decomposition, and whether the deviation patterns observed in reciprocal-regime solids encode geometric information not visible in their traditional descriptions.
RobertEdwardGrant.com